El Mathematica me pone de los nervios

No es fácil obtener las raíces de un polinomio cuando quieres mantener los parámetros como incógnitas. El objetivo: estudiar las condiciones de estabilidad de un sistema formado por proceso de primer orden más regulador PID discretos en bucle cerrado. Mi idea: obtener en Mathematica las expresiones de los polos del polinomio característico, en función de las componentes de ganancia (Kp), acción integral (Ki) y acción derivada (Kd), más el período de muestreo (Ts), y el polo de un proceso de primer orden (a). El resultado: un buen chorizo del que no se puede sacar nada en claro. 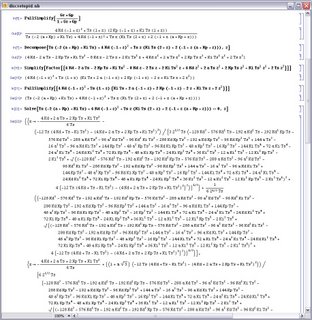Aquí fue cuando dije: "¡¡Aaaaaaaaaaargh!!". Siempre que abro el Mathematica tengo el temor de que me ocurra lo que al final casi siempre me ocurre:

1. Intento desarrollar unas ecuaciones en forma simbólica.
2. Me pego el curro definiéndolas.
3. Por mucho que busque comandos, no consigo que factorice o se simplifique o muestre los resultados en función de la variable que yo quiero.
4. Al final cojo boli y papel y las desarrollo yo mismo como a mí me gustan. O eso, o me pongo a asignar valores a parámetros a los que no quería asignar valores.

Es cierto que no soy ningún experto en Mathematica. Siempre que me pongo con estas cosas, echo mano del Help Browser para buscar los comandos, y es posible que alguna vez no los use adecuadamente o aprovechando todas sus posibilidades. Sin embargo, aún no he sido capaz de encontrar la combinación de sentencias que me permitan explicarle al Mathematica lo que quiero, algo así como: "Mathematica, ¿podrías simplificarme esta expresión y reformularla en raíces de z?. Te liberaré toda la RAM que tú quieras". ¿Es posible que la formulación esté mal expresada, o realmente le estoy pidiendo demasiado? [Trabajo][Investigación]